Cell Cycle

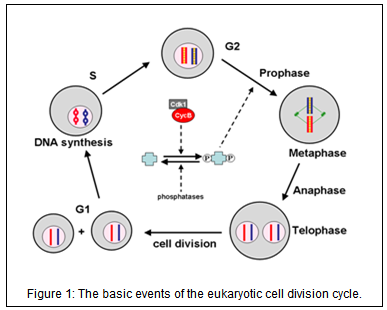
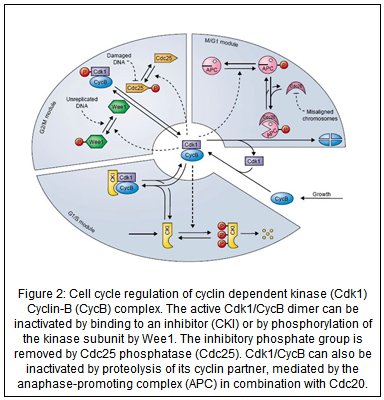
The basic events of the cell cycle are triggered by fluctuations in the activities of specific cyclin-dependent kinases (CDK). CDK activities are governed, in general, by three distinct mechanisms (Fig. 2):
(1) Cyclin availability. Kinase subunits are present in excess during the cell cycle, but they have no activity until they bind to a cyclin partner. The availability of cyclin subunits is strictly controlled by transcription factors that regulate the expression of cyclin genes, and by ubiquitin-dependent proteolysis systems (e.g., the APC—anaphase promoting complex) that can rapidly degrade cyclin proteins in response to specific signals.
(2) Phosphorylation of kinase subunits. Active cyclin:CDK dimers can be inactivated by phosphorylation on a specific tyrosine residue close to the N-terminus of the kinase polypeptide chain. This tyrosine residue is phosphorylated by kinases of the Wee1-class and dephosphorylated by phosphatases of the Cdc25-class.
(3) Active cyclin:CDK dimers can also be inactivated by binding to inhibitors, called CKIs. CKIs come and go, depending on their production rate (governed by regulated transcription factors) and destruction rate (phosphorylated CKIs are rapidly ubiquitinated and degraded).

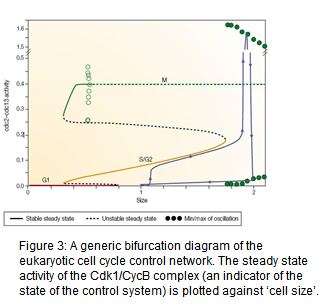
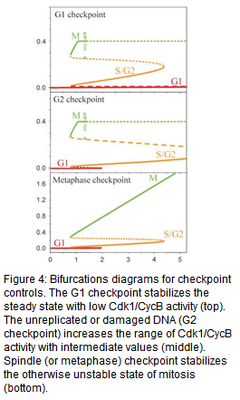
Using nonlinear ordinary differential equations, we have built successful computer models for cell cycle control network of budding and fission yeasts, frog and fruit fly embryos, and human cells. These models accurately reproduce the physiological properties of normal cell division, and the bizarre properties of mutant cells that have been studied. The models also predict phenotypes of novel mutants and unintuitive properties (bistability, hysteresis etc.) of the cell cycle machinery (see Fig. 3). The models also explain how checkpoint mechanisms block the control system when completion of certain cell cycle events (e.g. DNA replication, mitosis) is compromised (Fig. 4). Recently we became also interested in how cell cycle controls gets modified during the meiotic cycle when DNA replication is followed by two nuclear divisions.